题目内容
8.设数列{an}的前项和为Sn,若点An(n,$\frac{S_n}{n}}$)在函数f(x)=-x+c的图象上运动,其中c是与x无关的常数且a1=3.(1)求数列{an}的通项公式;
(2)设bn=tanan+1•tanan,tan195+tan3=atan2,求数列{bn}的前99项和(用含a的式子表示).
分析 (1)由点An(n,$\frac{S_n}{n}}$)在函数f(x)=-x+c的图象上运动,可得$\frac{{S}_{n}}{n}$=-n+c,即Sn=-n2+cn,由于c是与x无关的常数且a1=3.代入可得c,再利用递推关系即可得出.
(II)由tan(an+1-an)=$\frac{tan{a}_{n+1}-tan{a}_{n}}{1+tan{a}_{n+1}tan{a}_{n}}$,可得bn=tanan+1•tanan=-$\frac{tan{a}_{n+1}-tan{a}_{n}}{tan2}$-1.即可得出.
解答 解:(1)∵点An(n,$\frac{S_n}{n}}$)在函数f(x)=-x+c的图象上运动,∴$\frac{{S}_{n}}{n}$=-n+c,∴Sn=-n2+cn,
∵c是与x无关的常数且a1=3.∴3=-1+c,解答c=4.
∴Sn=-n2+4n.
∴n≥2时,an=Sn-Sn-1=-n2+4n-[-(n-1)2+4(n-1)]=-2n+5,n=1时也成立.
(II)∵tan(an+1-an)=$\frac{tan{a}_{n+1}-tan{a}_{n}}{1+tan{a}_{n+1}tan{a}_{n}}$,∴bn=tanan+1•tanan=$\frac{tan{a}_{n+1}-tan{a}_{n}}{tan(-2)}$-1=-$\frac{tan{a}_{n+1}-tan{a}_{n}}{tan2}$-1.
∴数列{bn}的前99项和T99=-$\frac{1}{tan2}[(tan{a}_{100}-tan{a}_{99})$+(tana99-tana98)+…+(tana2-tana1)]-99
=-$\frac{tan(-195)-tan3}{tan2}$-99
=a-99.
点评 本题考查了“裂项求和”方法、递推关系、和差公式,考查了推理能力与计算能力,属于中档题.

| A. | x-3y-5=0 | B. | 3x+y-5=0 | C. | x+3y-5=0 | D. | x-y-5=0 |
| A. | (1007$\sqrt{2}$,1007$\sqrt{2}$) | B. | (-1007$\sqrt{2}$,1007$\sqrt{2}$) | C. | (1007,1007$\sqrt{3}$) | D. | (1007$\sqrt{3}$,1007) |
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
(1)求b;
(2)有评估机构从以往购买了车险的车辆中随机抽取了1000辆调查,得到一年中出险次数的频数分布如下(并用相应频率估计2016年度出险次数的概率):
| 一年中出险的次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
| 空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
| 质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(2)若在(1)中,当t>300时,y与t的关系拟合与曲线 $\stackrel{∧}{y}$=a+blnt,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10)且知$\sum_{i=1}^{10}$lnti=70,$\sum_{i=1}^{10}$yi=6000,$\sum_{i=1}^{10}$yilnti=42500,$\sum_{i=1}^{10}$(lnti)2=500试用可线性化的回归方法,求拟合曲线的表达式
(附:线性回归方程$\stackrel{∧}{y}$=a+bx中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 广告费用x | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 58 |
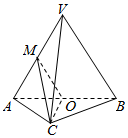 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.