题目内容
20.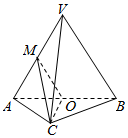 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;
(2)求证:CO⊥面VAB;
(3)求三棱锥C-VAB的体积.
分析 (1)由中位线定理得VB∥OM,故而VB∥平面MOC;
(2)由三线合一可知OC⊥AB,利用面面垂直的性质得出OC⊥平面VAB;
(3)由勾股定理求出AB,OC,得出△VAB的面积,代入棱锥的体积公式即可.
解答 证明:(1)∵O,M分别为AB,VA的中点,
∴VB∥OM,又VB?平面MOC,OM?平面MOC,
∴VB∥平面MOC.
(2)∵AC=BC,O是AB的中点,
∴OC⊥AB,
又平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,OC?平面ABC,
∴OC⊥平面VAB.
(3)∵AC⊥BC且AC=BC=$\sqrt{2}$,∴AB=2.
∴OC=$\frac{1}{2}$AB=1.
∵△VAB为等边三角形,
∴S△VAB=$\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$.
∴VC-VAB=$\frac{1}{3}{S}_{△VAB}•OC$=$\frac{1}{3}×\sqrt{3}×1$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
11.若圆x2+(y-1)2=r2与曲线(x-1)y=1没有公共点,则半径r的取值范围是( )
| A. | 0<r<$\sqrt{2}$ | B. | 0<r<$\frac{\sqrt{11}}{2}$ | C. | 0<r<$\sqrt{3}$ | D. | 0<r<$\frac{\sqrt{13}}{2}$ |
12.为了有效降低工业废气对大气的污染,某厂通过节能降耗技术改造来降低单位产量的能耗,通过统计得到了节能降耗技术改造后生产某产品的产量x(吨)与相应的生产能耗y(吨标准煤)的几组数据如表:
根据如表提供的数据,求出y关于x的回归线方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=0.7,则产量为8吨时相应的生产能耗(吨标准煤)为( )
| x | 2 | 3 | 4 | 5 |
| y | 1.5 | 2 | 3 | 3.5 |
| A. | 5.65 | B. | 6.45 | C. | 4.35 | D. | 5.05 |
9.已知x,y的取值如表所示:若y与x线性相关,且$\hat y=0.95x+2.6$,则a=4.3.
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | a | 4.8 | 6.7 |