题目内容
13.在某城市气象部门的数据中,随机抽取100天的空气质量指数的监测数据如表| 空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
| 质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(2)若在(1)中,当t>300时,y与t的关系拟合与曲线 $\stackrel{∧}{y}$=a+blnt,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10)且知$\sum_{i=1}^{10}$lnti=70,$\sum_{i=1}^{10}$yi=6000,$\sum_{i=1}^{10}$yilnti=42500,$\sum_{i=1}^{10}$(lnti)2=500试用可线性化的回归方法,求拟合曲线的表达式
(附:线性回归方程$\stackrel{∧}{y}$=a+bx中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
分析 (1)令y>200解出t的取值范围,根据频数分布表计算此范围内的频率,则此频率近似等于所求的概率;
(2)令x=lnt,利用回归系数公式求出y关于x的回归方程,再得出y关于t的拟合曲线.
解答 解:(1)令y>200得2t-100>200,解得t>150,
∴当t>150时,病人数超过200人.
由频数分布表可知100天内空气指数t>150的天数为25+15+10=50.
∴病人数超过200人的概率P=$\frac{50}{100}=\frac{1}{2}$.
(2)令x=lnt,则y与x线性相关,$\overline{x}$=$\frac{\sum_{i=1}^{10}ln{t}_{i}}{10}$=7,$\overline{y}=\frac{\sum_{i=1}^{10}{y}_{i}}{10}$=600,
∴b=$\frac{\sum_{i=1}^{10}{y}_{i}ln{t}_{i}-10\overline{x}\overline{y}}{\sum_{i=1}^{10}ln{{t}_{i}}^{2}-10{\overline{x}}^{2}}$=$\frac{42500-10×7×600}{500-10×49}$=50,a=600-50×7=250.
∴拟合曲线方程为y=50x+250=50lnt+250.
点评 本题考查了用样本的频率估计概率,可化为线性相关的回归方程的求解,属于中档题.

练习册系列答案
相关题目
1.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
根据上表得回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=-3.2,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$,据此回归方程估计零售价为5元时销售量估计为( )
| x | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 10 |
| A. | 16个 | B. | 20个 | C. | 24个 | D. | 28个 |
18.数列{an}满足a1=$\frac{1}{2}$,且对于任意n∈N+都满足an+1=$\frac{a_n}{{3{a_n}+1}}$,则数列{an•an+1}的前n项和为( )
| A. | $\frac{1}{3n+1}$ | B. | $\frac{n}{3n+1}$ | C. | $\frac{1}{3n-2}$ | D. | $\frac{n}{2(3n+2)}$ |
3.已知变量x和y满足关系y=-0.2x+3,变量y与z负相关.下列结论中正确的是( )
| A. | x与y负相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y正相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
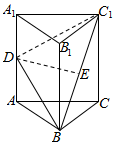 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.