题目内容
设数列{an}满足:a1=2,a2=8,an+2=(2+i2n)an+1+i2n,(i是虚数单位,n=1,2,3,…).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=na2n,n∈N+,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=na2n,n∈N+,求数列{bn}的前n项和Tn.
考点:数列的求和,复数代数形式的混合运算
专题:等差数列与等比数列
分析:(Ⅰ)当n是奇数时,an=
=2,当n是偶数时,an+2=3an+2,从而推导出{an+1}是以a2+1=9为首项,3为公比的等比数列,由此求出an=
.
(Ⅱ)bn=na2n=n(3n+1-1)=n•3n+1-n,由此利用分组求和法和错位相减法能求出数列{bn}的前n项和Tn.
| a | 1 |
|
(Ⅱ)bn=na2n=n(3n+1-1)=n•3n+1-n,由此利用分组求和法和错位相减法能求出数列{bn}的前n项和Tn.
解答:
解:(Ⅰ)∵数列{an}满足:a1=2,a2=8,an+2=(2+i2n)an+1+i2n,
①当n是奇数时,an=
=2,
②当n是偶数时,an+2=3an+2,∴an+2+1=3(an+1),
{an+1}是以a2+1=9为首项,3为公比的等比数列,
∴an+1=9•3
-1=3
+1,
∴an=3
+1-1.
由①②知,an=
.
(Ⅱ)由(Ⅰ)知a2n=3n+1-1,
∴bn=na2n=n(3n+1-1)=n•3n+1-n,
设{n•3n+1}的前n项和为Sn,
则Sn=1•32+2•33+3•34+…+n•3n+1,①
3Sn=1•33+2•34+3•35+…+n•3n+2,②
①-②,得-2Sn=32+33+34…+3n+1-n•3n+2
=
-n•3n+2,
∴Sn=
+
•3n+2,
∴Tn=
+
•3n+2-
.
①当n是奇数时,an=
| a | 1 |
②当n是偶数时,an+2=3an+2,∴an+2+1=3(an+1),
{an+1}是以a2+1=9为首项,3为公比的等比数列,
∴an+1=9•3
| n |
| 2 |
| n |
| 2 |
∴an=3
| n |
| 2 |
由①②知,an=
|
(Ⅱ)由(Ⅰ)知a2n=3n+1-1,
∴bn=na2n=n(3n+1-1)=n•3n+1-n,
设{n•3n+1}的前n项和为Sn,
则Sn=1•32+2•33+3•34+…+n•3n+1,①
3Sn=1•33+2•34+3•35+…+n•3n+2,②
①-②,得-2Sn=32+33+34…+3n+1-n•3n+2
=
| 32(1-3n) |
| 1-3 |
∴Sn=
| 9 |
| 4 |
| 2n-1 |
| 4 |
∴Tn=
| 9 |
| 4 |
| 2n-1 |
| 4 |
| n(n+1) |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
相关题目
 己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )
己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( ) 如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.
如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.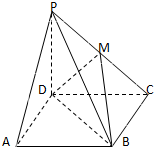 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.