题目内容
已知{an}是等比数列,a4•a7=-512,a3+a8=124,且公比为整数,则公比q为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由题设条件知a3和a8是方程x2-124x-512=0的两个实数根,解方程x2-124x-512=0,得x1=128,x2=-4,由公比q为整数,知a3=-4,a8=128,由此能够求出公比q.
解答:
解:∵{an}是等比数列,a4a7=-512,a3+a8=124,
∴a3a8=-512,a3+a8=124,
∴a3和a8是方程x2-124x-512=0的两个实数根,
解方程x2-124x-512=0,
得x1=128,x2=-4,
∵公比q为整数,
∴a3=-4,a8=128,
∴-4q5=128,解得q=-2,
故选:B.
∴a3a8=-512,a3+a8=124,
∴a3和a8是方程x2-124x-512=0的两个实数根,
解方程x2-124x-512=0,
得x1=128,x2=-4,
∵公比q为整数,
∴a3=-4,a8=128,
∴-4q5=128,解得q=-2,
故选:B.
点评:本题主要考查了等比数列的性质.若 m、n、p、q∈N*,且m+n=p+q,则aman=apaq.

练习册系列答案
相关题目
某校一社团共有10名成员,从周一到周五每天安排两人值日,若甲、乙必须排在同一天,且丙、丁不能排在同一天,则不同的安排方案共有( )
| A、21600 | B、10800 |
| C、7200 | D、5400 |
下列函数中,满足f(x-y)=
的单调递减函数是( )
| f(x) |
| f(y) |
| A、f(x)=x3 | ||
B、f(x)=x
| ||
C、f(x)=(
| ||
| D、f(x)=3x |
若cos2α=
,α∈(
,π),则sinα等于( )
| 7 |
| 8 |
| 3π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
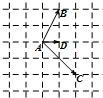 已知向量
已知向量| AC |
| AD |
| AB |
| AC |
| AB |
| AD |
| A、2 | B、-2 | C、3 | D、-3 |
 对一块边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=
对一块边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1= 己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )
己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( ) 如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.
如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.