题目内容
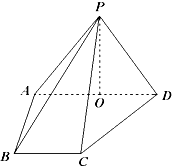 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=| 2 |
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为
| ||
| 2 |
| AQ |
| QD |
考点:点、线、面间的距离计算,异面直线及其所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)根据线面垂直的判定定理可知,只需证直线PO垂直平面ABCD中的两条相交直线垂直即可;
(2)先通过平移将两条异面直线平移到同一个起点B,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可;
(3)利用Vp-DQC=VQ-PCD,即可得出结论.
(2)先通过平移将两条异面直线平移到同一个起点B,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可;
(3)利用Vp-DQC=VQ-PCD,即可得出结论.
解答:
 (1)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
(1)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
所以PO⊥平面ABCD.
(2)解:连接BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(1)知PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=
,
在Rt△POA中,因为AP=
,AO=1,所以OP=1,
在Rt△PBO中,PB=
,所以cos∠PBO=
,
所以异面直线PB与CD所成的角的余弦值为
.
(3)解:假设存在点Q,使得它到平面PCD的距离为
.
设QD=x,则S△DQC=
x,由(2)得CD=OB=
,
在Rt△POC中,PC=
,
所以PC=CD=DP,S△PCD=
×(
)2=
,
由Vp-DQC=VQ-PCD,得x=
,所以存在点Q满足题意,此时
=
.
 (1)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
(1)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
所以PO⊥平面ABCD.
(2)解:连接BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(1)知PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=
| 2 |
在Rt△POA中,因为AP=
| 2 |
在Rt△PBO中,PB=
| 3 |
| ||
| 3 |
所以异面直线PB与CD所成的角的余弦值为
| ||
| 3 |
(3)解:假设存在点Q,使得它到平面PCD的距离为
| ||
| 2 |
设QD=x,则S△DQC=
| 1 |
| 2 |
| 2 |
在Rt△POC中,PC=
| 2 |
所以PC=CD=DP,S△PCD=
| ||
| 4 |
| 2 |
| ||
| 2 |
由Vp-DQC=VQ-PCD,得x=
| 3 |
| 2 |
| AQ |
| QD |
| 1 |
| 3 |
点评:本题主要考查直线与平面的位置关系、异面直线所成角、点到平面的距离等基本知识,考查空间想象能力,逻辑思维能力和运算能力.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.
如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.