题目内容
已知函数f(x)=
sin2x+
cos2x.
(1)求函数f(x)最大值和单调增区间;
(2)已知△ABC外接圆半径R=
,f(
-
)+f(
+
)=4
sinAsinB,角A,B所对的边分别是a,b,求a+b的最小值.
| 2 |
| 2 |
(1)求函数f(x)最大值和单调增区间;
(2)已知△ABC外接圆半径R=
| 3 |
| A |
| 2 |
| π |
| 8 |
| B |
| 2 |
| π |
| 8 |
| 6 |
考点:两角和与差的正弦函数,正弦函数的定义域和值域,余弦定理
专题:解三角形
分析:(1)对函数解析式化简,利用三角函数的性质求得函数的最大值和递增区间.
(2)根据已知等式求得sinA和sinB的关系式,再利用正弦定理转化为a和b的关系式,最后利用基本不等式求得a+b的最小值.
(2)根据已知等式求得sinA和sinB的关系式,再利用正弦定理转化为a和b的关系式,最后利用基本不等式求得a+b的最小值.
解答:
解:(1)f(x)=
sin2x+
cos2x=2sin(2x+
),
∴f(x)max=2,
由2kπ-
≤2x+
≤2kπ+
,得kπ-
≤x≤kπ+
(k∈Z),
∴函数的单调增区间为[kπ-
,kπ+
](k∈Z).
(2)依题意知2sin(A-
+
)+2sin(B+
+
)=2sinA+2cosB=4
sinAsinB,
∴
+
=2
,
∵△ABC外接圆半径R=
∴
=
,sinB=
,
∴
+
=2
∴a+b=
ab,
∵ab≤
,
∴
,求得a+b≥2
,a=b时取等号.
即a+b的最小值为2
.
| 2 |
| 2 |
| π |
| 4 |
∴f(x)max=2,
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数的单调增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(2)依题意知2sin(A-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 6 |
∴
| 1 |
| sinA |
| 1 |
| sinB |
| 6 |
∵△ABC外接圆半径R=
| 3 |
∴
| 1 |
| sinA |
2
| ||
| a |
2
| ||
| b |
∴
2
| ||
| a |
2
| ||
| b |
| 6 |
∴a+b=
| 2 |
∵ab≤
| (a+b)2 |
| 4 |
∴
| a+b≤ | ||
|
| (a+b)2 |
| 4 |
| 2 |
即a+b的最小值为2
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,正弦定理的运用.考查了学生基础知识的综合运用能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,在三棱锥A-BCD中,E,F分别是AB,CD的中点,试比较EF和
如图,在三棱锥A-BCD中,E,F分别是AB,CD的中点,试比较EF和 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=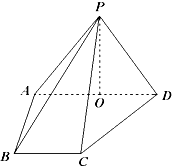 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=