题目内容
当x>0时,y=x+
的最小值是 .
| 1 |
| x |
考点:基本不等式
专题:不等式的解法及应用
分析:直接利用基本不等式求函数y=x+
的最小值.
| 1 |
| x |
解答:
解:∵x>0,
∴y=x+
≥2
=2.
当且仅当x=1时取“=”.
故答案为:2.
∴y=x+
| 1 |
| x |
x•
|
当且仅当x=1时取“=”.
故答案为:2.
点评:本题考查了基本不等式在求函数最值中的应用,利用基本不等式求函数最值,注意“一正、二定、三项等”,是基础题.

练习册系列答案
相关题目
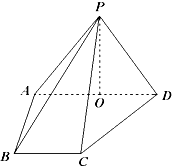 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=