题目内容
 如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.
如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.(1)求证:A1C1⊥平面MBD;
(2)当正方体棱长等于
| 3 |
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)分别证明出DM⊥A1C1和BM⊥A1C1,进而根据线面垂直的判定定理证明出A1C1⊥平面MBD;
(2)先求得M到BD的距离进而求得△MBD的面积,进而利用体积公式求得答案.
(2)先求得M到BD的距离进而求得△MBD的面积,进而利用体积公式求得答案.
解答:
解:
(1)证明:因为几何体是正方体ABCD-A1B1C1D1截取三棱锥B1-A1BC1后所得,
⇒A1C1⊥平面MBD;
(2)由题意知BD=
,点M到BD的距离为
,
则△MBD的面积为S△MBD=
×
×
=
,由(1)知A1C1⊥平面MBD
所以VD-A1BC1=
S△MBD•A1C1=
×
×
=
.
(1)证明:因为几何体是正方体ABCD-A1B1C1D1截取三棱锥B1-A1BC1后所得,
|
(2)由题意知BD=
| 6 |
| 3 |
则△MBD的面积为S△MBD=
| 1 |
| 2 |
| 6 |
| 3 |
3
| ||
| 2 |
所以VD-A1BC1=
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 2 |
| 6 |
| 3 |
点评:本小题以正方体为载体,考查立体几何的基础知识.本题通过分层设计,考查了空间直线与平面的垂直关系,简单几何体体积的求法,考查学生的空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图,在三棱锥A-BCD中,E,F分别是AB,CD的中点,试比较EF和
如图,在三棱锥A-BCD中,E,F分别是AB,CD的中点,试比较EF和 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=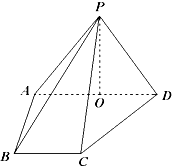 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=