题目内容
已知函数f（x）=
+
（a∈N+），设f（x）的最大值、最小值分别为m，n，若m-n＜2，则正整数a的取值个数是 ．
| 2a-x |
| x |
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：由(
)2≤
求函数的最大值，由单调性求最小值，解不等式求a．
| ||||
| 2 |
| ||||
| 2 |
解答：
解：f（x）=
+
，
则由(
)2≤
得，
f（x）=
+
≤2
．（当且仅当x=a时，等号成立）
则m=2
．
f（x）min=f（0）=f（2a）=
=n，
则由m-n＜2得，
2
-
＜2，
化简解得，0≤a＜6+4
又∵11＜6+4
＜12，a∈N+
则a=1，2，3，…，11．
故正整数a的取值个数是11．
故答案为11．
| 2a-x |
| x |
则由(
| ||||
| 2 |
| ||||
| 2 |
f（x）=
| 2a-x |
| x |
| a |
则m=2
| a |
f（x）min=f（0）=f（2a）=
| 2a |
则由m-n＜2得，
2
| a |
| 2a |
化简解得，0≤a＜6+4
| 2 |
又∵11＜6+4
| 2 |
则a=1，2，3，…，11．
故正整数a的取值个数是11．
故答案为11．
点评：本题考查了不等式的综合应用，属于中档题．
练习册系列答案
口算题天天练系列答案
相关题目
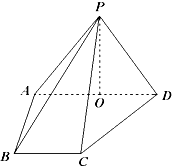如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=