题目内容
13.在数列{an}中,满足点P(an,an+1)是函数f(x)=3x图象上的点,且a1=3.(1)求{an}的通项公式;
(2)若bn=nan,求数列{bn}的前n项和Sn.
分析 (1)通过将点P(an,an+1)代入函数方程f(x)=3x化简可知an+1=3an,进而可知数列{an}是首项为3、公比为3的等比数列,进而计算可得结论;
(2)通过(1)可知bn=n3n,进而利用错位相减法计算即得结论.
解答 解:(1)∵点P(an,an+1)是函数f(x)=3x图象上的点,
∴an+1=3an,
又∵a1=3,
∴数列{an}是首项为3、公比为3的等比数列,
∴其通项公式an=3n;
(2)由(1)可知bn=nan=n3n,
∴Sn=1×3+2×32+…+n3n,
3Sn=1×32+2×33+…+(n-1)3n+n×3n+1,
错位相减得:-2Sn=3+32+…+3n-n×3n+1
=3×$\frac{1-{3}^{n}}{1-3}$-n×3n+1
=$\frac{1-2n}{2}$×3n+1-$\frac{3}{2}$,
∴Sn=$\frac{2n-1}{4}$×3n+1+$\frac{3}{4}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.下列各图中,不可能表示函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
4.方程${log_{\frac{1}{2}}}x={2^x}-2016$的实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
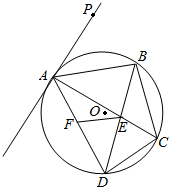 已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.
已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.