题目内容
14.已知z=$\frac{1+i}{\sqrt{2}}$,i是虚数单位,则1+|z|+z50+z100=1+i.分析 化简可得z=$\frac{1+i}{\sqrt{2}}$=cos$\frac{π}{4}$+isin$\frac{π}{4}$,从而可得1+|z|+z50+z100=1+1+cos$\frac{50π}{4}$+isin$\frac{50π}{4}$+cos(25π)+isin(25π).
解答 解:z=$\frac{1+i}{\sqrt{2}}$=cos$\frac{π}{4}$+isin$\frac{π}{4}$,
故1+|z|+z50+z100
=1+1+cos$\frac{50π}{4}$+isin$\frac{50π}{4}$+cos(25π)+isin(25π)
=2+i-1=1+i;
故答案为:1+i.
点评 本题考查了复数的模及复数的运算的应用.

练习册系列答案
相关题目
4.方程${log_{\frac{1}{2}}}x={2^x}-2016$的实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
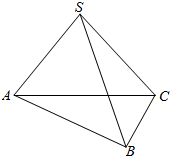
 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.