题目内容
函数f(x)=
(0≤x≤2且x∈N+)的值域是 .
| 1+x |
| 2+x |
考点:函数的值域
专题:函数的性质及应用
分析:直接利用函数的解析式,根据函数的定义域求出函数的值.
解答:
解:f(x)=
=1-
(0≤x≤2且x∈N+)
则:f(1)=1-
=
f(2)=1-
=
所以函数的值域为:{
,
}
故答案为:{
,
}
| 1+x |
| 2+x |
=1-
| 1 |
| x+2 |
(0≤x≤2且x∈N+)
则:f(1)=1-
| 1 |
| 3 |
| 2 |
| 3 |
f(2)=1-
| 1 |
| 4 |
| 3 |
| 4 |
所以函数的值域为:{
| 2 |
| 3 |
| 3 |
| 4 |
故答案为:{
| 2 |
| 3 |
| 3 |
| 4 |
点评:本体考察的知识点:利用函数的解析式求函数的值,及相关的运算问题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| 2△x |
A、
| ||
| B、f′(x0) | ||
| C、2f′(x0) | ||
| D、-f′(x0) |
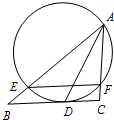 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.