题目内容
5.设极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴.已知曲线C的极坐标方程为ρ=8sinθ(1)求曲线C的直角坐标方程;
(2)设直线$\left\{\begin{array}{l}x=t\\ y=t+2\end{array}\right.$(t为参数)与曲线C交于A,B两点,求AB的长.
分析 (1)曲线C的极坐标方程为ρ=8sinθ,即ρ2=8ρsinθ.利用互化公式可得曲线C的直角坐标方程.
(2)设直线$\left\{\begin{array}{l}x=t\\ y=t+2\end{array}\right.$(t为参数)的直角坐标方程为y=x+2.x2+y2=8y,配方为x2+(y-4)2=16,可得圆心C(0,4),半径r=4.求出圆心C到直线的距离d.可得|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:(1)曲线C的极坐标方程为ρ=8sinθ,即ρ2=8ρsinθ.
∴曲线C的直角坐标方程为x2+y2=8y.
(2)设直线$\left\{\begin{array}{l}x=t\\ y=t+2\end{array}\right.$(t为参数)的直角坐标方程为y=x+2.
x2+y2=8y,配方为x2+(y-4)2=16,可得圆心C(0,4),半径r=4.
∴圆心C到直线的距离d=$\frac{|0-4+2|}{\sqrt{2}}$=$\sqrt{2}$.
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{14}$.
点评 本题考查了极坐标方程化为直角坐标方程、点到直线的距离公式公式、直线与圆直角弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.已知幂函数y=f(x)过点(2,8),则f(3)=( )
| A. | 27 | B. | 9 | C. | 8 | D. | 4 |
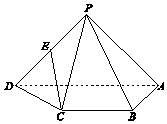 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1