题目内容
13.设不等式$\left\{\begin{array}{l}x≥1\\ x-y≤0\\ x+y≤4\end{array}\right.$表示的平面区域为M,若直线y=kx-2上存在M内的点,则实数k的取值范围是[2,5].分析 由题意,做出不等式组对应的可行域,由于函数y=kx+1的图象是过点A(0,-2),斜率为k的直线l,故由图即可得出其范围..
解答 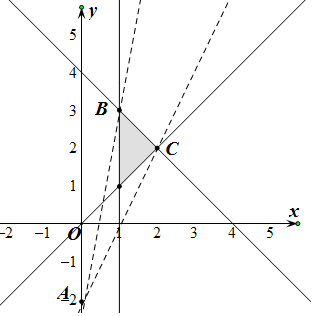 解:由约束条件$\left\{\begin{array}{l}x≥1\\ x-y≤0\\ x+y≤4\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}x≥1\\ x-y≤0\\ x+y≤4\end{array}\right.$作出可行域如图,
如图.因为函数y=kx-2的图象是过点A(0,-2),且斜率为k的直线l,
由图知,当直线l过点B(1,3)时,
k取最大值$\frac{3+2}{1-0}$=5,
当直线l过点C(2,2)时,k取最小值$\frac{2+2}{2-0}$=2,
故实数k的取值范围是[2,5].
故答案为:[2,5].
点评 本题考查简单线性规划,利用线性规划的知识用图象法求出斜率的最大值与最小值.这是一道灵活的线性规划问题,还考查了数形结合的思想,属中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
1.已知双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的一个焦点是(2,0),则其渐近线的方程为( )
| A. | x±$\sqrt{3}$y=0 | B. | $\sqrt{3}$x±y=0 | C. | x±3y=0 | D. | 3x±y=0 |
18.设P为有公共焦点F1,F2的椭圆C1与双曲线C2的一个交点,且PF1⊥PF2,椭圆C1的离心率为e1,双曲线C2的离心率为e2,若3e1=e2,则e1=$\frac{\sqrt{5}}{3}$.
12.学校计划在周一至周四的艺术节上展演《雷雨》、《茶馆》、《天籁》和《马蹄声碎》四部话剧,每天一部.受多种因素影响,话剧《雷雨》不能在周一和周四上演;《茶馆》不能在周一和周三上演;《天籁》不能在周三和周四上演;《马蹄声碎》不能在周一和周四上演.那么下列说法正确的是( )
| A. | 《雷雨》只能在周二上演 | B. | 《茶馆》可能在周二或周四上演 | ||
| C. | 周三可能上演《雷雨》或《马蹄声碎》 | D. | 四部话剧都有可能在周二上演 |