题目内容

10．已知幂函数y=f（x）过点（2，8），则f（3）=（　　）
A．27B．9C．8D．4

分析 把点（2，3）代入函数解析式列出方程求出α的值，即可求出函数的解析式，从而求出函数值即可．

解答 解：因为幂函数y=f（x）=xα过点（2，8），
所以8=2α，解得α=3，
故f（x）=x3，f（3）=27，
故选：A．

点评 本题考查利用待定系数法求幂函数的解析式，属于基础题．

练习册系列答案
相关题目
20．已知点F为抛物线y2=2px（p＞0）的焦点，点M（2，m）在抛物线E上，且|MF|=3．
（1）求抛物线E的方程；
（2）过x轴正半轴上一点N（a，0）的直线与抛物线E交于A，B两点，若OA⊥OB，求a的值．
1．已知双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的一个焦点是（2，0），则其渐近线的方程为（　　）
A．x±$\sqrt{3}$y=0B．$\sqrt{3}$x±y=0C．x±3y=0D．3x±y=0
18．设P为有公共焦点F1，F2的椭圆C1与双曲线C2的一个交点，且PF1⊥PF2，椭圆C1的离心率为e1，双曲线C2的离心率为e2，若3e1=e2，则e1=$\frac{\sqrt{5}}{3}$．
5．设极坐标系的极点为直角坐标系的原点，极轴为x轴的正半轴．已知曲线C的极坐标方程为ρ=8sinθ
（1）求曲线C的直角坐标方程；
（2）设直线$\left\{\begin{array}{l}x=t\\ y=t+2\end{array}\right.$（t为参数）与曲线C交于A，B两点，求AB的长．
15．函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x+3，x＞-1}\\{{2}^{x+1}-1，x≤-1}\end{array}\right.$，已知f（a）=3，则a的值是（　　）
A．0B．-2C．0或-2D．1
2．已知函数f（x）=2cos2x+$\sqrt{3}$sin2x，x∈R．
（1）求函数f（x）的最小正周期及单调递增区间；
（2）当x∈（$\frac{π}{12}$，$\frac{π}{3}$）时，求f（x）的值域．
8．已知函数f（x）对任意实数x，y均有f（x）=f（$\frac{x+y}{2}$）+f（$\frac{x-y}{2}$）．当x＞0时，f（x）＞0
（1）判断函数f（x）在R上的单调性并证明；
（2）设函数g（x）与函数f（x）的奇偶性相同，当x≥0时，g（x）=|x-m|-m（m＞0），若对任意x∈R，不等式g（x-1）≤g（x）恒成立，求实数m的取值范围．
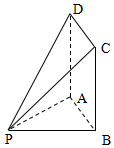9．如图，四边形ABCD为矩形，PB=2，BC=3，PA⊥平面ABCD．
（1）证明：平面PCD⊥平面PAD；
（2）当AB的长为多少时，点B到平面ACD的距离为$\frac{3}{2}$？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网