题目内容
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1的短轴的一个端点B与两焦点F1,F2组成三角形的周长为8+8$\sqrt{2}$,且F1B⊥F2B,求椭圆方程.分析 当椭圆的焦点在x轴上,设椭圆的焦点为(±c,0),由题意可得,2a+2c=8+8$\sqrt{2}$,2c=$\sqrt{2}$a,解方程可得a,c,再由a,b,c的关系,计算即可得到所求方程,同理可得焦点在y轴上的方程.
解答 解:当椭圆的焦点在x轴上,设椭圆的焦点为(±c,0),
由题意可得,2a+2c=8+8$\sqrt{2}$,
2c=$\sqrt{2}$a,
解方程可得a=4$\sqrt{2}$,c=4,b=$\sqrt{{a}^{2}-{c}^{2}}$=4,
可得椭圆的方程为$\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1;
当椭圆的焦点在y轴上,设椭圆的焦点为(0,±c),
由题意可得2b+2c=8+8$\sqrt{2}$,
2c=$\sqrt{2}$b,
解方程可得b=4$\sqrt{2}$,c=4,a=$\sqrt{{b}^{2}-{c}^{2}}$=4,
可得椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{32}$=1.
综上可得,椭圆的方程为$\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1或$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{32}$=1.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质和方程思想,考查运算能力,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.函数f(x)=-4x3+6x2+1在[0,3]上的最大值为( )
| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
2.$\frac{sin20°cos20°}{cos50°}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
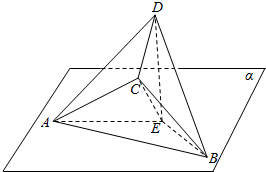 如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.
如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.