题目内容
将正方体截去一个四棱柱后得到的几何体的正视图与俯视图如图所示,则该几何体的侧视图为( )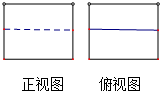

A、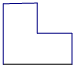 |
B、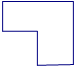 |
C、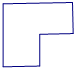 |
D、 |
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:根据几何体三视图“长对正,高平齐,宽相等”的原则,由几何体的正视图与俯视图,可得几何体的三视图,进而得到答案.
解答:
解:根据几何体三视图“长对正,高平齐,宽相等”的原则,
由几何体的正视图与俯视图,
可得几何体的三视图如下所示:

故选:D
由几何体的正视图与俯视图,
可得几何体的三视图如下所示:

故选:D
点评:本题考查的知识点是简单空间图形的三视图,熟练掌握几何体三视图“长对正,高平齐,宽相等”的原则,是解答的关键.

练习册系列答案
相关题目
若函数f(x)=5sin(ωx+
)(ω>0)与g(x)=2sin(2x+φ)(0<φ<π)的图象有相同的对称轴,则函数g(x)的一个单调区间为( )
| π |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[π,
|
若如图所给程序框图运行的结果恰为s>
,那么判断框中可以填入的关于k的判断条件是( )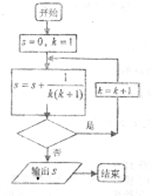
| 2012 |
| 2013 |

| A、k>2013 |
| B、k>2012 |
| C、k<2013 |
| D、k<2012 |
一个几何体的三视图如图所示,则该几何体的体积、表面积为( )
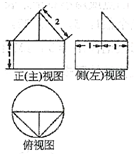

A、π+
| ||||||||
B、2π+
| ||||||||
C、π+
| ||||||||
D、2π+
|
随机写出两个小于1的正数x与y,它们与数1一起形成一个三元数组(x,y,1).这样的三元数组正好是
一个钝角三角形的三边的概率是( )
一个钝角三角形的三边的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
现安排甲、乙等5名同学去参加3个运动项目,要求每个项目都有人参加,每人只参加一个项目,则满足上述要求且甲、乙两人不参加同一个项目的安排方法种数为( )
| A、114 | B、162 |
| C、108 | D、132 |

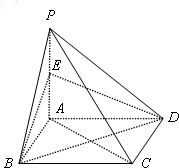 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.