题目内容
8.已知函数f(x)=ax+xlnx的图象在点A(e,f(e))处的切线斜率为3(1)求a的值;
(2)求f(x)的单调区间;
(3)若不等式f(x)-kx+k>0对任意x∈(1,+∞)恒成立,求k的最大整数值.
分析 (1)由已知条件推导出f'(x)=a+lnx+1,a+lne+1=3,由此能求出a=1.
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(3)由f(x)=x+xlnx,得k<$\frac{x+xlnx}{x-1}$对任意x∈(1,+∞)恒成立,由此利用构造法结合导数性质能求出整数k的最大值.
解答 解:(1)因为f(x)=ax+xlnx,所以f'(x)=a+lnx+1,
因为函数f(x)=ax+xlnx的图象在点A处的切线斜率为3,
所以,f'(e)=3,即a+lne+1=3,
所以,a=1;
(2)由(1)得:f(x)=x+xlnx,函数的定义域是(0,+∞),f′(x)=lnx+2,
令f′(x)>0,解得:x>e-2,令f′(x)<0,解得:0<x<e-2,
故f(x)在(0,e-2)递减,在(e-2,+∞)递增;
(3)由(1)知,f(x)=x+xlnx,
所以,k<$\frac{f(x)}{x-1}$对任意x>1恒成立,
即k<$\frac{x+xlnx}{x-1}$对任意x>1恒成立,
令g(x)=$\frac{x+xlnx}{x-1}$,则g′(x)=$\frac{x-lnx-2}{{(x-1)}^{2}}$,
令h(x)=x-lnx-2(x>1),则h′(x)=$\frac{x-1}{x}$>0,
所以函数h(x)在(1,+∞)上单调递增,
而h(1)=-1<0,h(3)=1-ln3<0,h(4)=2(1-ln2)>0,
故存在x0∈(3,4)使得h(x0)=0,
所以g(x)在(1,x0)递减,在(x0,+∞)递增,
而g(3)=$\frac{3(1+ln3)}{2}$>3,g(4)=$\frac{4(1+2ln2)}{3}$<4,
故整数k的最大值是3.
点评 本题考查实数值的求法,考查整数的最大值的求法,解题时要认真审题,注意构造法和导数性质的合理运用.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有平面A′GF⊥平面BCED | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
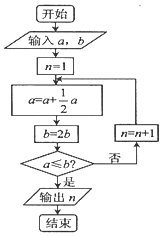 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | y=$\frac{1}{x}$ | B. | y=|x|-1 | C. | y=lg x | D. | y=($\frac{1}{2}$)|x| |