题目内容
13.已知函数$f(x)={(\frac{1}{3})^x}-{log_2}$x,正实数a,b,c是公差为负数的等差数列,且满足f(a)•f(b)•f(c)<0,若实数d是方程f(x)=0的一个解,那么下列四个判断:①d<a;②d<b;③d>c;④d<c中一定成立的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由条件和等差数列的性质判断出a、b、c的大小关系,由题意画出$y={(\frac{1}{3})}^{x}和y=lo{g}_{2}^{x}$的图象,通过方程的根与图象交点问题,由图象可得答案.
解答 解:∵正实数a,b,c是公差为负数的等差数列,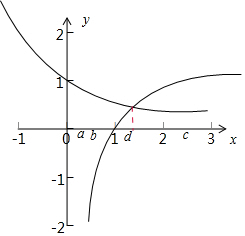
∴0<a<b<c,
在坐标系中画出$y={(\frac{1}{3})}^{x}和y=lo{g}_{2}^{x}$的图象:
∵f(a)•f(b)•f(c)<0,
且实数d是方程f(x)=0的一个解,
∴由图可得,a<d<c一定成立,
则①d<a不正确;②d<b不一定;
③d>c不正确;④d<c正确,
∴一定成立的个数是1个,
故选A.
点评 本题考查等差数列的性质,指数函数、对数函数的图象,以及过方程的根与图象交点问题的转化,考查转化思想、数形结合思想.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
3.已知x∈R,则“x>2”是“x2-3x+2>0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.等差数列{an}中,a2+a3+a4=3,Sn为等差数列{an}的前n项和,则S5=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.股票市场的前身是起源于1602年荷兰人在阿姆斯特河大桥上进行荷属东印度公司股票的买卖,而正规的股票市场最早出现在美国.2017年2月26号,中国证监会主席刘士余谈了对股市的几点建议,给广大股民树立了信心.最近,张师傅和李师傅要将家中闲置资金进行投资理财.现有两种投资方案,且一年后投资盈亏的情况如下:
(1)投资股市:
(2)购买基金:
(Ⅰ)当$p=\frac{1}{2}$时,求q的值;
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
(1)投资股市:
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | p | $\frac{1}{3}$ | q |
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
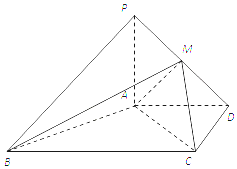 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.