等差数列{an}中.a2+a3+a4=3.Sn为等差数列{an}的前n项和.则S5=( )A．3B．4C．5D．6 题目和参考答案——青夏教育精英家教网—

题目内容

1．等差数列{a_n}中，a₂+a₃+a₄=3，S_n为等差数列{a_n}的前n项和，则S₅=（　　）

A．

B．

C．

D．

分析由等差数列通项公式得a₂+a₃+a₄=3a₃=3，从而a₃=1，再由等差列前n项和公式得S₅=$\frac{5}{2}（{a}_{1}+{a}_{5}）$=5a₃，由此能求出结果．

解答解：∵等差数列{a_n}中，a₂+a₃+a₄=3，
S_n为等差数列{a_n}的前n项和，
∴a₂+a₃+a₄=3a₃=3，
解得a₃=1，
∴S₅=$\frac{5}{2}（{a}_{1}+{a}_{5}）$=5a₃=5．
故选：C．

点评本题考查等差数列的前5项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案

相关题目

11．执行如图所示的程序框图，则输出的结果是（　　）

12．已知圆M与y轴相切，圆心在直线y=$\frac{1}{2}$x上，并且在x轴上截得的弦长为2$\sqrt{3}$．则圆M的标准方程为（x-2）²+（y-1）²=4或（x+2）²+（y+1）²=4．

9．

如图，在平面直角坐标系xOy中，焦点在x轴上的椭圆C：$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点（b，2e），其中e为椭圆C的离心率．过点T（1，0）作斜率为k（k＞0）的直线l交椭圆C于A，B两点（A在x轴下方）．
（1）求椭圆C的标准方程；
（2）过点O且平行于l的直线交椭圆C于点M，N，求 $\frac{AT•BT}{MN2}$ 的值；
（3）记直线l与y轴的交点为P．若$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{TB}$，求直线l的斜率k．

16．如图，程序输出的结果s=1320，则判断框中应填（　　）

6．

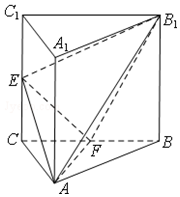如图，三棱柱ABC-A₁B₁C₁中，侧棱AA₁⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AA₁=AB=2，E，F分别是CC₁，BC的中点．
（1）求证：平面AB₁F⊥平面AEF；
（2）求点C到平面AEF的距离．

13．已知函数$f（x）={（\frac{1}{3}）^x}-{log_2}$x，正实数a，b，c是公差为负数的等差数列，且满足f（a）•f（b）•f（c）＜0，若实数d是方程f（x）=0的一个解，那么下列四个判断：①d＜a；②d＜b；③d＞c；④d＜c中一定成立的个数为（　　）

10．

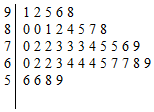中国诗词大会的播出引发了全民的读书热，某小学语文老师在班里开展了一次诗词默写比赛，班里40名学生得分数据的茎叶图如图所示．若规定得分不小于85分的学生得到“诗词达人”的称号，小于85分且不小于70分的学生得到“诗词能手”的称号，其他学生得到“诗词爱好者”的称号，根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生，则抽选的学生中获得“诗词能手”称号的人数为（　　）

9．一个袋中装有3个红球和1个白球，现从袋中取出1球，然后放回袋中再取出一球，则两次取出的球颜色相同的概率是$\frac{5}{8}$．

试题分类