题目内容
7．若函数$y={（\frac{1}{5}）^{x+1}}+m$的图象不过第一象限，则实数m的取值范围是（-∞，-$\frac{1}{5}$]．分析 根据指数函数的图象和性质即可得到结论．
解答 解：∵函数f（x）为减函数，且函数f（x）的图象不经过第一象限，
则满足f（0）=$\frac{1}{5}$+m≤0，即m≤-$\frac{1}{5}$；
故答案为：（-∞，-$\frac{1}{5}$]．
点评 本题主要考查指数函数的图象和性质，比较基础．
练习册系列答案
相关题目
17．以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F，且与y轴交于P、Q两点．若△MPQ为正三角形，则该双曲线的离心率为（ ）
| A． | 4 | B． | $\sqrt{7}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
18．设直线x-3y+t=0（t≠0）与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线分别交于点A，B．若点M（t，0）满足|MA|=|MB|，则双曲线的渐近线方程为（ ）
| A． | y=±4x | B． | y=±2x | C． | y=±$\frac{1}{2}$x | D． | y=±$\frac{1}{4}$x |
15．在（1+x）（2+x）5的展开式中，x3的系数为（ ）
| A． | 75 | B． | 100 | C． | 120 | D． | 130 |
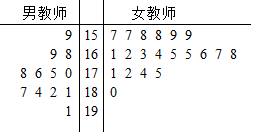新疆某中学共有教师32人，其中男教师12人，女教师20人，这32名教师的身高如下面的茎叶图所示（单位：cm）．为“打击疆独分子，确保学校师生安全”，校委会决定：身高在175cm以上（含175cm）的男教师和身高在172cm以上（含172cm）的女教师组成“校外巡逻队”，其余教师组成“校内巡逻队”．