题目内容
16.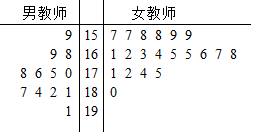 新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.
新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.(1)若用分层抽样的方法从“校外巡逻队员”和“校内巡逻队员”中抽取中选8人,然后在从这8人中选3人,求至少有1人是“校外巡逻队员”的概率;
(2)若从所有“校外巡逻队员”中选2人作为“校外巡逻队”队长,用X表示“校外巡逻队”队长为女教师的人数,试写出X的分布列,并求X的数学期望.
分析 (1)由茎叶图得“校外巡逻队员”有12人,“校内巡逻队员”有20人,用分层抽样在“校外巡逻队员”选3人,“校内巡逻队员”中选5人,由此能求出从这8人中选3人,至少有1人是“校外巡逻队员”的概率.
(2)由题意X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(1)由茎叶图得身高在175cm以上(含175cm)的男教师有8人,身高在172cm以上(含172cm)的女教师有4人,
∴“校外巡逻队员”有12人,“校内巡逻队员”有20人,
用分层抽样的方法从“校外巡逻队员”和“校内巡逻队员”中抽取中选8人,
则“校外巡逻队员”选:$\frac{8}{32}×12$=3人,“校内巡逻队员”选:$\frac{8}{32}×20$=5人,
从这8人中选3人,至少有1人是“校外巡逻队员”的概率:
p=1-$\frac{{C}_{5}^{3}}{{C}_{8}^{3}}$=1-$\frac{10}{56}$=$\frac{23}{28}$.
(2)由题意X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{8}^{2}}{{C}_{12}^{2}}$=$\frac{28}{66}$=$\frac{14}{33}$,
P(X=1)=$\frac{{C}_{8}^{1}{C}_{4}^{1}}{{C}_{12}^{2}}$=$\frac{32}{66}$=$\frac{16}{33}$,
P(X=2)=$\frac{{C}_{4}^{2}}{{C}_{12}^{2}}$=$\frac{6}{66}$=$\frac{1}{11}$,
∵X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{14}{33}$ | $\frac{16}{33}$ | $\frac{1}{11}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

 阅读快车系列答案
阅读快车系列答案某农科所为了深入研究海拔因素对青蒿素产量的影响,在山上和山下的试验田中分别种植了100 株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了4株青蒿作为样本,每株提取的青蒿素产量(单位:克)如表所示:
| 编号 位置 | ① | ② | ③ | ④ |
| 山上 | 5.0 | 3.8 | 3.6 | 3.6 |
| 山下 | 3.6 | 4.4 | 4.4 | 3.6 |
(Ⅱ)记山上与山下两块试验田单株青蒿素产量的方差分别为$s_1^2$,$s_2^2$,根据样本数据,试估计$s_1^2$与$s_2^2$的大小关系(只需写出结论);
(Ⅲ)从样本中的山上与山下青蒿中各随机选取1 株,记这2 株的产量总和为ξ,求随机变量ξ的分布列和数学期望.
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |