题目内容
8.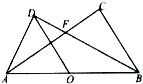 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.(1)证明:A,B,C,D四点共圆,且O为圆心;
(2)AC与BD相交于点F,若BC=2CF=6,AF=5,求C,D之间的距离.
分析 (1)利用△ABC与△ABD都是以AB为斜边的直角三角形,可得A,B,C,D四点都在以AB为直径的圆上,证明O是AB的中点,可得O为圆心;
(2)由Rt△ADF∽Rt△BCF得$\frac{AD}{DF}$=$\frac{BC}{CF}$=2,由BD平分∠ABC得$\frac{BD}{DA}$=$\frac{BC}{CF}$=2,求出AD,即可得出结论.
解答  (1)证明:因为△ABC与△ABD都是以AB为斜边的直角三角形,
(1)证明:因为△ABC与△ABD都是以AB为斜边的直角三角形,
所以A,B,C,D四点都在以AB为直径的圆上.
因为BD平分∠ABC,且OD∥BC,
所以∠OBD=∠CBD=∠ODB,OB=OD.
又∠OAD+∠OBD=90°,∠ODA+∠ODB=90°,
所以∠OAD=∠ODA,OA=OD.
所以OA=OB,O是AB的中点,O为圆心.…(5分)
(2)解:由BC=2CF=6,得BF=3$\sqrt{5}$,
由Rt△ADF∽Rt△BCF得$\frac{AD}{DF}$=$\frac{BC}{CF}$=2.
设AD=2DF=2x,则AF=$\sqrt{5}$x,
由BD平分∠ABC得$\frac{BD}{DA}$=$\frac{BC}{CF}$=2,
所以$\frac{3\sqrt{5}+x}{2x}$=2,解得x=$\sqrt{5}$,即AD=2$\sqrt{5}$.
连CD,由(1),CD=AD=2$\sqrt{5}$.…(10分)
点评 本题考查四点共圆的证明,考查三角形相似的判定与性质,考查角平分线的性质,属于中档题.

练习册系列答案
相关题目
20.设集合A={1,2,3},B={0,1,2},则A∪B中元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
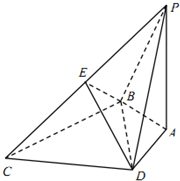 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.