题目内容
19.实验中学学生会将在5月份对各部进行改选,劳动部现从高一甲、乙、丙、丁四个人中选两名劳动部长,则甲被选中的概率为$\frac{1}{2}$.分析 先求出基本事件总数n=${C}_{4}^{2}$=6,再求出甲被选中包含怕基本事件个数m=${C}_{1}^{1}{C}_{3}^{1}=3$,由此能求出甲被选中的概率.
解答 解:实验中学学生会将在5月份对各部进行改选,
劳动部现从高一甲、乙、丙、丁四个人中选两名劳动部长,
基本事件总数n=${C}_{4}^{2}$=6,
甲被选中包含怕基本事件个数m=${C}_{1}^{1}{C}_{3}^{1}=3$,
∴甲被选中的概率为p=$\frac{m}{n}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
7.抛物线y2=8x的焦点坐标是( )
| A. | (-2,0) | B. | (0,-2) | C. | (2,0) | D. | (0,2) |
14.已知圆C的参数方程为$\left\{\begin{array}{l}{x=-1+cosα}\\{y=1+sinα}\end{array}\right.$ (α为参数),当圆心C到直线kx+y+4=0的距离最大时,k的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{5}$ |
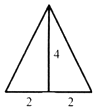
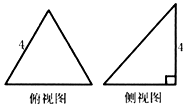 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )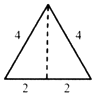
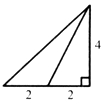
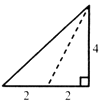
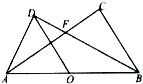 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.


