题目内容
20.设集合A={1,2,3},B={0,1,2},则A∪B中元素的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用并集定义直接求解.
解答 解:∵集合A={1,2,3},B={0,1,2},
∴A∪B={0,1,2,3},其中有4个元素.
故选:C.
点评 本题考查并集的求法,是基础题,解题时要认真审题,注意并集性质的合理运用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15.已知集合A={x|x2-x-6<0},B={x|$\frac{x+4}{x-2}$>0},则A∩B等于( )
| A. | (-2,3) | B. | (2,3) | C. | (-4,-2) | D. | (-4,3) |
5.已知函数f(x)=$\frac{1}{3}$x3+x2+ax.若g(x)=$\frac{1}{e^x}$,对任意x1∈[$\frac{1}{2}$,2],存在x2∈[$\frac{1}{2}$,2],使f'(x1)≤g(x2)成立,则实数a的取值范围是( )
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
12.函数y=$\frac{k}{x}$的图象经过点(-4,6),则下列各点中在y=$\frac{k}{x}$图象上的是( )
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |
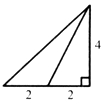
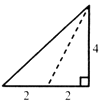
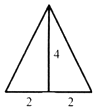
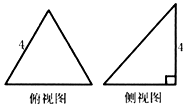 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )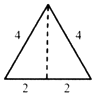
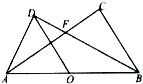 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.


