题目内容
17.求值化简:(1)$\frac{{1+\frac{1}{2}lg9-lg240}}{{1-\frac{2}{3}lg27+lg\frac{36}{5}}}$+1
(2)$\frac{{{{({a^{\frac{2}{3}}}•{b^{-1}})}^{-\frac{1}{2}}}•{a^{\frac{1}{2}}}•{b^{\frac{1}{3}}}}}{{\root{6}{{a•{b^5}}}}}$.
分析 (1)利用对数的运算性质即可得出.
(2)利用指数的运算性质即可得出.
解答 解:(1)原式=$\frac{1+lg\frac{3}{240}}{1-lg9+lg\frac{36}{5}}$+1=$\frac{lg\frac{1}{8}}{lg(\frac{36}{5}×10×\frac{1}{9})}$+1=-1+1=0.
(2)原式=$\frac{{a}^{-\frac{1}{3}+\frac{1}{2}}•{b}^{\frac{1}{2}+\frac{1}{3}}}{{a}^{\frac{1}{6}}{b}^{\frac{5}{6}}}$=a0b0=1.
点评 本题考查了指数幂与对数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
7.抛物线y2=8x的焦点坐标是( )
| A. | (-2,0) | B. | (0,-2) | C. | (2,0) | D. | (0,2) |
5.已知函数f(x)=$\frac{1}{3}$x3+x2+ax.若g(x)=$\frac{1}{e^x}$,对任意x1∈[$\frac{1}{2}$,2],存在x2∈[$\frac{1}{2}$,2],使f'(x1)≤g(x2)成立,则实数a的取值范围是( )
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
12.函数y=$\frac{k}{x}$的图象经过点(-4,6),则下列各点中在y=$\frac{k}{x}$图象上的是( )
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |
2.若函数f(x)是定义在R上的偶函数,在(-∞,0)上对任意两个不相等的实数a,b总有$\frac{f(a)-f(b)}{a-b}$>0,且f(2)=0,则使xf(x)<0的x的取值范围是( )
| A. | -2<x<2 | B. | x>2或-2<x<0 | C. | -2<x<0 | D. | x<-2或x>2 |
6.设全集U={-1,1,3,5,7},集合A={1,|3-a|,5},若∁UA={-1,7},则实数a的值是( )
| A. | 0 | B. | 6 | C. | -4或10 | D. | 0或6 |
7.命题:“对任意 x>0,ex>x+1”的否定是( )
| A. | 存在 x≤0,ex≤x+1 | B. | 存在 x>0,ex≤x+1 | ||
| C. | 存在 x≤0,ex>x+1 | D. | 对任意 x>0,ex≤x+1 |
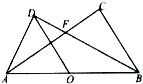 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.


