题目内容
3.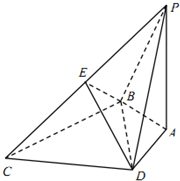 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.(1)求AB;
(2)求点E到平面PBD的距离.
分析 (1)由PA⊥底面ABCD,可得PA⊥BC,结合已知可得BC⊥平面PAB,得到AB⊥BC,连接AC,由已知求解在直角三角形可得AB=2;
(2)由(1)求得BC=BD=2$\sqrt{3}$,PB=PD=$2\sqrt{3}$,由E为PC的中点,得PC⊥平面BED,设点E到平面PBD的距离为h,利用等积法,由VP-BDE=VE-PBD,求得点E到平面PBD的距离.
解答 解:(1)∵PA⊥底面ABCD,BC?平面ABCD,∴PA⊥BC,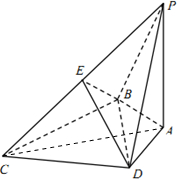
又∵PB⊥BC,PA∩PB=P,∴BC⊥平面PAB,
∵AB?平面PAB,∴AB⊥BC
∵△BCD为等边三角形,又AB=AD,连接AC,
则∠ACB=30°,设AB=x,则AC=2x,
又PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,PA=2$\sqrt{2}$,
∴$\frac{2\sqrt{2}}{2x}=\frac{\sqrt{2}}{2}$,得x=2,即AB=2;
(2)由(1)求得BC=BD=2$\sqrt{3}$,PB=PD=$2\sqrt{3}$,
∵E为PC的中点,∴DE⊥PC,BE⊥PC,即PC⊥平面BED,
∵$PB=PB=BD=2\sqrt{3}$,∴${S}_{△PBD}=\frac{1}{2}×2\sqrt{3}×3=3\sqrt{3}$,
∵AC=4,PA=2$\sqrt{2}$,∴$PC=\sqrt{{4}^{2}+(2\sqrt{2})^{2}}=2\sqrt{6}$,则PE=$\sqrt{6}$,
∴$DE=BE=\sqrt{(2\sqrt{3})^{2}-(\sqrt{6})^{2}}=\sqrt{6}$,则${S}_{△BDE}=\frac{1}{2}×2\sqrt{3}×\sqrt{3}=3$.
设点E到平面PBD的距离为h,
由VP-BDE=VE-PBD,得$\frac{1}{3}×3×\sqrt{6}=\frac{1}{3}×3\sqrt{3}h$,解得h=$\sqrt{2}$.
∴点E到平面PBD的距离为$\sqrt{2}$.
点评 本题考查点、线、面间的距离计算,考查了空间想象能力和思维能力,是中档题.

 口算题天天练系列答案
口算题天天练系列答案| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({-1,\frac{1}{2}})$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{5}$ |

| A. | $6+2\sqrt{2}+\sqrt{6}$ | B. | $6+2\sqrt{2}$ | C. | 3 | D. | $\frac{8}{3}$ |
| A. | (-2,3) | B. | (2,3) | C. | (-4,-2) | D. | (-4,3) |
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |
| A. | 2019 届的优秀学生 | B. | 高一数学必修一课本上的所有难题 | ||
| C. | 遵义四中高一年级的所有男生 | D. | 比较接近 1 的全体正数 |
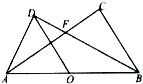 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.