题目内容
16.设a,b∈R,c∈[0,2π),若对任意实数x都有2sin(3x-$\frac{π}{3}$)=asin(bx+c),定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点横坐标为d,则满足条件的有序实数组(a,b,c,d)的组数为28.分析 首先由已知等式求得a值,然后利用三角恒等变换sin2x=cosx求出所有根的个数,最后利用排列组合的思想求得满足条件的有序实数组.
解答 解:∵对任意实数x都有2sin(3x-$\frac{π}{3}$)=asin(bx+c),∴|a|=2,
若a=2,则方程等价于sin(3x-$\frac{π}{3}$)=sin(bx+c),则函数的周期相同,
若b=3,此时c=$\frac{5π}{3}$;若b=-3,此时c=$\frac{4π}{3}$;
若a=-2,则方程等价于sin(3x-$\frac{π}{3}$)=-sin(bx+c)=sin(-bx-c),
若b=-3,此时c=$\frac{π}{3}$;若b=3,此时c=$\frac{2π}{3}$.
综上,满足条件的数组(a,b,c,)为(2,3,$\frac{5π}{3}$),(2,-3,$\frac{4π}{3}$),
(-2,-3,$\frac{π}{3}$),(-2,3,$\frac{2π}{3}$)共4组.
而当sin2x=cosx时,2sinxcosx=cosx,得cosx=0或sinx=$\frac{1}{2}$,
∴x=$\frac{π}{2}$+kπ或x=$\frac{π}{6}$+2kπ,k∈Z
又∵x∈[0,3π],∴x=$\frac{π}{2},\frac{3π}{2},\frac{5π}{2},\frac{π}{6},\frac{13π}{6},\frac{5π}{6},\frac{17π}{6}$.
∴满足条件的有序数组(a,b,c,d)共有4×7=28.
故答案为28.
点评 本题考查三角函数的周期性、三角函数的恒等变换及三角函数的图象和性质,考查渗透转化与化归思想方法,是中档题.

练习册系列答案
相关题目
17.“sinα=cosα”是“$α=\frac{π}{4}+2kπ,(k∈Z)$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.抛物线y2=8x的焦点坐标是( )
| A. | (-2,0) | B. | (0,-2) | C. | (2,0) | D. | (0,2) |
5.已知函数f(x)=$\frac{1}{3}$x3+x2+ax.若g(x)=$\frac{1}{e^x}$,对任意x1∈[$\frac{1}{2}$,2],存在x2∈[$\frac{1}{2}$,2],使f'(x1)≤g(x2)成立,则实数a的取值范围是( )
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
6.设全集U={-1,1,3,5,7},集合A={1,|3-a|,5},若∁UA={-1,7},则实数a的值是( )
| A. | 0 | B. | 6 | C. | -4或10 | D. | 0或6 |
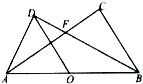 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.