题目内容
4.已知$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=($\sqrt{3}$,-1).(Ⅰ)若$\overrightarrow{a}$∥$\overrightarrow{b}$,求sin2x-6cos2x的值;
(Ⅱ)若f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,求函数f(2x)的单调减区间.
分析 (Ⅰ)根据向量的平行和角的三角函数的关系即可求出答案,
(Ⅱ)先求出f(x),再得到f(2x)的解析式,根据正弦函数的性质即可得到函数的单调减区间.
解答 解:(Ⅰ)∵$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=($\sqrt{3}$,-1),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴-sinx=$\sqrt{3}$cosx,
∴tanx=-$\sqrt{3}$,
∴sin2x-6cos2x=$\frac{si{n}^{2}x-6co{s}^{2}x}{si{n}^{2}x+co{s}^{2}x}$=$\frac{ta{n}^{2}x-6}{ta{n}^{2}x+1}$=$\frac{3-6}{3+1}$=-$\frac{3}{4}$,
(Ⅱ)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}$sinx-cosx=2sin(x-$\frac{π}{6}$),
∴f(2x)=2sin(2x-$\frac{π}{6}$),
∴$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{3}{2}$π+2kπ,k∈Z,
∴$\frac{π}{3}$+kπ≤x≤$\frac{5π}{6}$+kπ,k∈Z.
∴函数f(2x)的单调减区间[$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ],k∈Z.
点评 本题考查了向量的平行和向量的数量积以及三角函数的化简和正弦函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设Sn是等差数列{an}的前n项和,且a11=S13=13,则a9=( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
13.已知函数f(x)的定义域是R,f(0)=2,对任意x∈R,f′(x)>f(x)+1,则下列正确的为( )
| A. | (f(1)+1)•e>f(2)+1 | B. | 3e<f(2)+1 | ||
| C. | 3•e≥f(1)+1 | D. | 3e2与f(2)+1大小不确定 |
14.若函数f(x)为区间D上的凸函数,则对于D上的任意n个值x1、x2、…、xn,总有f(x1)+f(x2)+…+f(xn)≤nf($\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$),现已知函数f(x)=sinx在[0,$\frac{π}{2}$]上是凸函数,则在锐角△ABC中,sinA+sinB+sinC的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
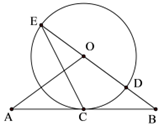 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.