题目内容
11.若x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≥0}\\{x+2y-4≥0}\\{x-3y-4≤0}\end{array}\right.$,则z=x2+y2的最小值为5.分析 画出满足条件的平面区域,求出角点的坐标,结合z=x2+y2的几何意义求出其最小值即可.
解答  解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{x-y-1=0}\\{x+2y-4=0}\end{array}\right.$,解得A(2,1),
z=x2+y2的几何意义表示平面区域内的点到原点的距离的平方,
故z=z=x2+y2=4+1=5,
故答案为:5.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
1.设a>0,b>0( )
| A. | 若lna+2a=lnb+3b,则a>b | B. | 2a+2a=2b+3b,则a<b | ||
| C. | 若lna-2a=lnb-3b,则a>b | D. | 2a-2a=2b-3b,则a<b |
19.复数z=$\frac{2}{1+i}$(i是虚数单位)的共轭复数在复平面内对应的点是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
3.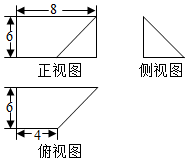 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |
1.已知复数z=a+bi(a,b∈R),则z∈R的充要条件是( )
| A. | a+bi=a-bi | B. | a+bi=-a+bi | C. | ab=0 | D. | a=b=0 |