题目内容
已知数列{an}的各项均为正数,对任意n∈N*,它的前n项和Sn满足Sn=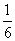 (an+1)(an+2),并且a2,a4,a9成等比数列.
(an+1)(an+2),并且a2,a4,a9成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=(-1)n+1anan+1,Tn为数列{bn}的前n项和,求T2n.
解 (1)∵对任意n∈N*,有Sn=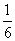 (an+1)(an+2), ①
(an+1)(an+2), ①
∴当n=1时,有S1=a1=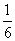 (a1+1)(a1+2),
(a1+1)(a1+2),
解得a1=1或2.
当n≥2时,有Sn-1=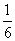 (an-1+1)(an-1+2). ②
(an-1+1)(an-1+2). ②
①-②并整理得(an+an-1)(an-an-1-3)=0.
而数列{an}的各项均为正数,∴an-an-1=3.
当a1=1时,an=1+3(n-1)=3n-2,
此时a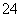 =a2a9成立;
=a2a9成立;
当a1=2时,an=2+3(n-1)=3n-1,
此时a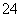 =a2a9不成立,舍去.
=a2a9不成立,舍去.
∴an=3n-2,n∈N*.
(2)T2n=b1+b2+…+b2n
=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
=-6a2-6a4-…-6a2n
=-6(a2+a4+…+a2n)
=-6×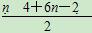 =-18n2-6n.
=-18n2-6n.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 展开式中各项系数之和为32,则该展开式中含
展开式中各项系数之和为32,则该展开式中含 的项的系数为
的项的系数为  开始以速度
开始以速度 运动,则此点前3秒所走过的路程为
运动,则此点前3秒所走过的路程为 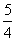 ,则数列{an}的通项公式为( )
,则数列{an}的通项公式为( )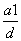 的值为( )
的值为( )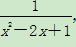 ,x∈(0,3),则( )
,x∈(0,3),则( )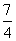 B.f(x)有最小值-1
B.f(x)有最小值-1