题目内容
已知{an}为等差数列，且a3＝－6，a6＝0.
(1)求{an}的通项公式；
(2)若等比数列{bn}满足b1＝－8，b2＝a1＋a2＋a3，求{bn}的前n项和公式．
解 (1)设等差数列{an}的公差为d.
因为a3＝－6，a6＝0，
所以
解得a1＝－10，d＝2.
所以an＝－10＋(n－1)×2＝2n－12.
(2)设等比数列{bn}的公比为q.
因为b2＝a1＋a2＋a3＝－24，b1＝－8，
所以－8q＝－24，q＝3.
所以数列{bn}的前n项和公式为
Sn＝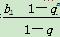
＝4(1－3n)．
练习册系列答案
相关题目
f(x)=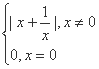 
则关于x的方程
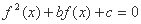有5个不同实数解的充要条件是 ( )
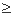-2 且 c=0
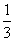，bn－1＝27bn(n≥2且n∈N＋)，若an＋logkbn为常数，则满足条件的k值( )
，
，
，
，
，
，
，
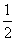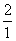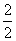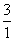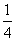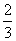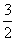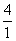，…，则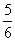
是数列中的( )
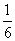(an＋1)(an＋2)，并且a2，a4，a9成等比数列．
a12的值为( )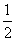
，－
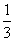]，则不等式x2－bx－a<0的解是( )
，则不等式f(x)≥x2的解集是( )