题目内容
设双曲线经过点(-2,0),且离心率e=
.
(1)求此双曲线的标准方程;
(2)求双曲线的焦点坐标及渐近线方程.
| ||
| 2 |
(1)求此双曲线的标准方程;
(2)求双曲线的焦点坐标及渐近线方程.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由题意,a=2,c=
,求出b,即可得出双曲线的标准方程;
(2)求出a,b,c,即可求出双曲线的焦点坐标及渐近线方程.
| 5 |
(2)求出a,b,c,即可求出双曲线的焦点坐标及渐近线方程.
解答:
解:(1)由题意,a=2,c=
,
∴b=1,
∴双曲线的标准方程
-y2=1;
(2)双曲线的焦点坐标(±
,0),渐近线方程为y=±
x.
| 5 |
∴b=1,
∴双曲线的标准方程
| x2 |
| 4 |
(2)双曲线的焦点坐标(±
| 5 |
| 1 |
| 2 |
点评:本题考查双曲线的标准方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)=
若f(x0-1)<1,则x的取值范围是( )
|
| A、(0,10) |
| B、(-1,+∞) |
| C、(-∞,-2)∪(-1,0) |
| D、(1,11) |
下图中可以表示函数图象的是( )
A、 |
B、 |
C、 |
D、 |
棱长都相等的正棱锥不可能是( )
| A、正三棱锥 | B、正四棱锥 |
| C、正五棱锥 | D、正六棱锥 |
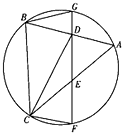 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.