题目内容
已知函数f（x）=cosx，则它可以由y=f′（x）的图象按照下列哪种交换得到（ ）
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由y=f′（x）=-sinx=sin（-x）=cos（x+
），可知把y=f′（x）的图象向右平移
个单位可以得到函数f（x）=cosx的图象．
| π |
| 2 |
| π |
| 2 |
解答：
解：∵f（x）=cosx，
∵y=f′（x）=-sinx=sin（-x）=cos（x+
）
∴把y=f′（x）的图象向右平移
个单位可以得到函数f（x）=cosx的图象，
故选：A．
∵y=f′（x）=-sinx=sin（-x）=cos（x+
| π |
| 2 |
∴把y=f′（x）的图象向右平移
| π |
| 2 |
故选：A．
点评：本题主要考查诱导公式的应用，y=Asin（ωx+φ）的图象变化规律，属于基础题．
练习册系列答案
计算高手系列答案
相关题目
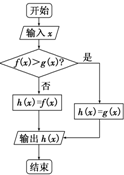
如图，若f（x）=logx3，g（x）=log2x，输入x=0.25，则输出h（x）=（ ）
| A、0.25 | ||
| B、2log32 | ||
C、-
| ||
| D、-2 |
若a=（
）cos2，b=logπ3，c=log2sin
，则（ ）
| 1 |
| 2 |
| 2π |
| 5 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |