题目内容
设椭圆
+
=1(a>b>0)的左焦点为F,短轴上端点为B,连接BF并延长交椭圆于点A,连接AO并延长交椭圆于点D,过B、F、O三点的圆的圆心为C.
(1)若C的坐标为(-1,1),求椭圆方程和圆C的方程;
(2)若AD为圆C的切线,求椭圆的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若C的坐标为(-1,1),求椭圆方程和圆C的方程;
(2)若AD为圆C的切线,求椭圆的离心率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意可得三角形BFO外接圆圆心为斜边BF中点C,由此求得b,c的值,结合隐含条件求出a,则椭圆方程和圆C的方程可求;
(2)由AD为圆C的切线,得到AD⊥CO,联立直线和椭圆方程求得A的坐标,由
•
=0得到a,b,c的关系式,结合隐含条件可求椭圆的离心率.
(2)由AD为圆C的切线,得到AD⊥CO,联立直线和椭圆方程求得A的坐标,由
| OA |
| OC |
解答:
解:(1)∵三角形BFO为直角三角形,
∴其外接圆圆心为斜边BF中点C,
由C点坐标为(-1,1)得,b=2,c=2,
∴a2=b2+c2=8,
则圆半径r=CO=
,
∴椭圆方程为
+
=1,
圆方程为(x+1)2+(y-1)2=2;
(2)由AD与圆C相切,得 AD⊥CO,
BF方程为y=
x+b,
由
,
得A(-
,-
),
由
•
=0,得b4=2a2c2,
(a2-c2)2=2a2c2a4-4a2c2+c4=0,
解得:e=
=
-
.
∴其外接圆圆心为斜边BF中点C,
由C点坐标为(-1,1)得,b=2,c=2,
∴a2=b2+c2=8,
则圆半径r=CO=
| 2 |
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
圆方程为(x+1)2+(y-1)2=2;
(2)由AD与圆C相切,得 AD⊥CO,
BF方程为y=
| b |
| c |
由
|
得A(-
| 2a2c2 |
| c(a2+c2) |
| b3 |
| a2+c2 |
由
| OA |
| OC |
(a2-c2)2=2a2c2a4-4a2c2+c4=0,
解得:e=
2-
|
| ||
| 2 |
| ||
| 2 |
点评:本题考查了椭圆与圆的方程的求法,考查了直线与圆锥曲线的关系,解答此题的关键是由平面几何知识得到对应的关系,考查了学生的计算能力,是中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则?p:?x∈R,x2-x+1≠0 |
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” |
| C、若y=f(x)为偶函数,则y=f(x+2 )的图象关于直线x=-2对称 |
| D、“a=1”是“函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数”的充要条件 |
已知曲线C的方程为x2-xy+y2-2=0,则下列各点中,在曲线C上的点是( )
A、(0,
| ||
| B、(1,-2) | ||
| C、(2,-3) | ||
| D、(3,8) |
已知A为圆A:(x-1)2+y2=25的圆心,平面上点P满足PA=
,那么点P与圆A的位置关系是( )
| 3 |
| A、点P在圆A上 |
| B、点P在圆A内 |
| C、点P在圆A外 |
| D、无法确定 |
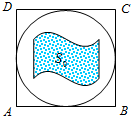 如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法:
如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法: