题目内容
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则?p:?x∈R,x2-x+1≠0 |
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” |
| C、若y=f(x)为偶函数,则y=f(x+2 )的图象关于直线x=-2对称 |
| D、“a=1”是“函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数”的充要条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.写出命题p:?x∈R,x2-x+1=0的否定,可判断A;
B.写出命题“若a=0,则ab=0”的否命题可判断B;
C.利用偶函数的性质(其图象关于y轴对称)及函数的图象的平移变换可判断C;
D.利用充分必要条件的概念可从充分性与必要性两个方面分析判断D.
B.写出命题“若a=0,则ab=0”的否命题可判断B;
C.利用偶函数的性质(其图象关于y轴对称)及函数的图象的平移变换可判断C;
D.利用充分必要条件的概念可从充分性与必要性两个方面分析判断D.
解答:
解:A:若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0,故A正确;
B:命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,故B正确;
C:若y=f(x)为偶函数,其图象关于y轴对称,而y=f(x+2 )的图象是将y=f(x)的图象向左平移一个单位得到的,故其图象关于直线x=-2对称,即C正确;
D:当a=1时,f(x)=x2-2x+1,其对称轴为x=1,故y=f(x)在区间[1,+∞)上是增函数,充分性成立;
反之,若函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数,则a≤1,即必要性不成立,故“a=1”是“函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数”的充分不必要条件,故D错误.
故选:D.
B:命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,故B正确;
C:若y=f(x)为偶函数,其图象关于y轴对称,而y=f(x+2 )的图象是将y=f(x)的图象向左平移一个单位得到的,故其图象关于直线x=-2对称,即C正确;
D:当a=1时,f(x)=x2-2x+1,其对称轴为x=1,故y=f(x)在区间[1,+∞)上是增函数,充分性成立;
反之,若函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数,则a≤1,即必要性不成立,故“a=1”是“函数f(x)=x2-2ax+1在区间[1,+∞)上是增函数”的充分不必要条件,故D错误.
故选:D.
点评:本题考查命题的真假判断与应用,综合考查命题及其否定,四种命题之间的关系及真假判断,考查充分必要条件及函数的奇偶性、图象平移变换等基础知识,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
设全集U=R,集合A={x|x≥0},B={x|-1<x<3},则(∁UA)∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<1} |
| C、{x|-3<x<0} |
| D、{x|x≥3} |
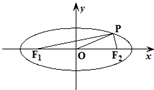 如图,F1、F2是椭圆
如图,F1、F2是椭圆