题目内容
7．若幂函数f（x）的图象经过点（2，$\frac{1}{4}$），则f（3）=$\frac{1}{9}$．分析 先用待定系数法求出幂函数的解析式，再求函数的值即可．
解答 解：设幂函数y=xα（α∈R），
其函数图象经过点（2，$\frac{1}{4}$），
∴2α=$\frac{1}{4}$；
解得α=-2，
∴y=f（x）=x-2；
∴f（3）=$\frac{1}{9}$，
故答案为：$\frac{1}{9}$．
点评 本题考查了求幂函数的解析式以及求函数值的问题，是基础题目．
练习册系列答案
相关题目
17．命题“?x0∈R，x02+x0-1＜0”的否定是（ ）
| A． | ?x∈R，x2+x-1≥0 | B． | ?x∈R，x2+x-1＜0 | ||
| C． | ?x0∈R，x02+x0-1≥0 | D． | ?x0∈R，x02+x0-1＞0 |
2．设U={1，2，3，4，5}，A={1，2，5}，B={2，3，4}，则B∩∁UA=（ ）
| A． | ∅ | B． | {2} | C． | {3，4} | D． | {1，3，4，5} |
12．设{an}是公比为q的等比数列，则“q＞1”是“{an}为单调递增数列”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
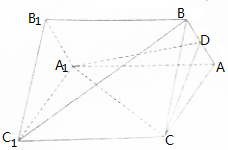如图，在直三棱柱ABC-A1B1C1中，D是AB的中点．