题目内容
18.2016年某招聘会上,有5个条件很类似的求职者,把他们记为A,B,C,D,E,他们应聘秘书工作,但只有2个秘书职位,因此5人中仅有2人被录用,如果5个人被录用的机会相等,分别计算下列事件的概率:(1)C得到一个职位
(2)B或E得到一个职位.
分析 (1)利用列举法求出5人中有2人被录用的基本事件共有10个,C得到一职位包含的基本事件有4个,由此能求出C得到一个职位的概率.
(2)利用列举法求出B或E得到一个职位,包含的基本事件个数,由此能求出B或E得到一个职位的概率.
解答 解:(1)5人中有2人被录用的基本事件共有10个,分别为:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),
C得到一职位包含的基本事件有4个,分别为(A,C),(B,C),(C,D),(C,E),
∴C得到一个职位的概率P1=$\frac{4}{10}=\frac{2}{5}$.
(2)B或E得到一个职位,包含的基本事件个数有7个,分别为:
(A,B),(A,E),(B,C),(B,D),(B,E),(C,E),(D,E),
∴B或E得到一个职位的概率P2=$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
3.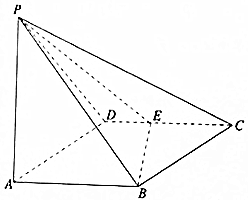 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B-PE-D的余弦值.
 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B-PE-D的余弦值.
10.函数f(x)=-x3+ax2-x-1在R上不单调,则实数a的取值范围是( )
| A. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | B. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
15.函数y=(x2-1)2+2的极值点是( )
| A. | x=1 | B. | x=-1或0 | C. | x=-1或1或0 | D. | x=0或1 |