题目内容
12．设{an}是公比为q的等比数列，则“q＞1”是“{an}为单调递增数列”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据等比数列的性质，结合充分条件和必要条件的定义进行判断即可得到结论．
解答 解：等比数列-1，-2，-4，…，满足公比q=2＞1，但{an}不是递增数列，充分性不成立．
若an=-1•（$\frac{1}{2}$）n-1为递增数列，但q=$\frac{1}{2}$＞1不成立，即必要性不成立，
故“q＞1”是“{an}为递增数列”的既不充分也不必要条件，
故选：D．
点评 本题主要考查充分条件和必要条件的判断，利用等比数列的性质，利用特殊值法是解决本题的关键．
练习册系列答案
相关题目
2．函数f（x）=xlnx的单调递减区间为（ ）
| A． | $（0，\frac{1}{e}）$ | B． | $（-∞，\frac{1}{e}）$ | C． | （-∞，-e） | D． | $（\frac{1}{e}，+∞）$ |
3．
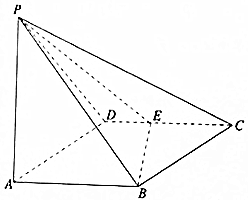如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．
（Ⅰ）证明：平面PBE⊥平面PAB；
（Ⅱ）求二面角B-PE-D的余弦值．
如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．（Ⅰ）证明：平面PBE⊥平面PAB；
（Ⅱ）求二面角B-PE-D的余弦值．
8．已知直线l经过点（0，-2），其倾斜角的大小是60°，则直线l与两坐标轴围成三角形的面积S等于（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{3\sqrt{3}}}{3}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |
9．
如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为$4\sqrt{3}$，则这个圆锥的体积为（ ）
如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为$4\sqrt{3}$，则这个圆锥的体积为（ ）| A． | $\frac{{\sqrt{15}}}{3}$ | B． | $\frac{{32\sqrt{35}π}}{27}$ | C． | $\frac{{128\sqrt{2}π}}{81}$ | D． | $\frac{{8\sqrt{3}}}{3}$ |