题目内容
6.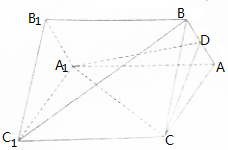 如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.(1)求证:BC1∥平面A1CD;
(2)若AA1=AC=CB=5,AB=6,求三棱锥D-AA1C的体积.
分析 (1)连结AC1,A1C,交于点O,连结OD,则OD∥BC1,由此能证明BC1∥平面A1CD.
(2)三棱锥D-AA1C的体积${V}_{D-A{A}_{1}C}$=${V}_{{A}_{1}-ADC}$,由此能求出结果.
解答 证明:(1) 连结AC1,A1C,交于点O,连结OD,
连结AC1,A1C,交于点O,连结OD,
∵在直三棱柱ABC-A1B1C1中,D是AB的中点.
∴OD∥BC1,∵OD?平面A1CD,BC1?平面A1CD,
∴BC1∥平面A1CD.
解:(2)∵在直三棱柱ABC-A1B1C1中,D是AB的中点,AA1=AC=CB=5,AB=6,
∴A1A⊥ADC,S△ADC=$\frac{1}{2}AD•DC$=$\frac{1}{2}×3×\sqrt{25-9}$=6,
∴三棱锥D-AA1C的体积:
${V}_{D-A{A}_{1}C}$=${V}_{{A}_{1}-ADC}$=$\frac{1}{3}×{A}_{1}A×{S}_{△ADC}$=$\frac{1}{3}×5×6$=10.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,考查空间想象能力、推理论证能力、数形结合思想、转化思想以及计算能力,是中档题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.函数f(x)=-x3+ax2-x-1在R上不单调,则实数a的取值范围是( )
| A. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | B. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
1.已知函数f(x)=log2(x+3)-2x3+4x的图象在[-2,5]内是连续不断的,对应值表如下:
(1)计算上述表格中的对应值a和b.
(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | a | -1 | 1.58 | b | -5.68 | -39.42 | -109.19 | -227 |
(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.
15.函数y=(x2-1)2+2的极值点是( )
| A. | x=1 | B. | x=-1或0 | C. | x=-1或1或0 | D. | x=0或1 |