题目内容
如图,多面体 的直观图及三视图如图所示,
的直观图及三视图如图所示, 分别
分别
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求多面体 的体积;
的体积;
(3)求证: .
.
 |
(1)证明:由多面体 的三视图知,
的三视图知,
 三棱柱
三棱柱 中,底面
中,底面 是等腰直
是等腰直
角三角形, ,
, 平面
平面 ,
,
侧面 都是边长为
都是边长为 的正方形.
的正方形.
连结 ,则
,则 是
是 的中点,
的中点,
在△ 中,
中, ,
,
且
 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面 .
.
(2) 因为 平面
平面 ,
,
 平面
平面 ,
,
 ,
,
又 ⊥
⊥ ,所以,
,所以, ⊥平面
⊥平面 ,
,
∴四边形  是矩形,
是矩形,
且侧面 ⊥平面
⊥平面
取 的中点
的中点



 ,
, ,
,
且 平面
平面 .
.
所以多面体 的体积
的体积 .
.
(3)∵ 平面
平面 ,
, ∥
∥ ,
,
∴ 平面
平面 ,
,
∴ ,
,
∵面 是正方形,
是正方形,
∴ ,
,
∴ ,
,
∴ .(本题也可以选择用向量的方法去解决)
.(本题也可以选择用向量的方法去解决)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,则
,则 的值为 ;
的值为 ; 的中心,则直线EF与面ABC所成的角的大小为
的中心,则直线EF与面ABC所成的角的大小为 B
B C
C D
D
 满足条件
满足条件 ,那么
,那么 的最大值为____________ .
的最大值为____________ .
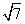 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为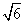 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为__________
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为__________ 中
中 ,则其前3项的和
,则其前3项的和 的取值范围是 .
的取值范围是 .