题目内容
某几何体的一条棱长为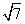，在该几何体的正视图中，这条棱的投影是长为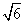的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为__________
4
如图，棱锥的底面是矩形，⊥平面，，为棱上一点，且.
（Ⅰ）求二面角的余弦值；
（Ⅱ）求点到平面的距离.
若椭圆的左右焦点分别为，线段被抛物线的焦点分成的两段，过点C(-1,0)且以向量为方向向量的直线交椭圆于不同两点A,B，满足
(1) 求椭圆的离心率；
(2) 当三角形OAB的面积最大时，求椭圆的方程。
如图，多面体的直观图及三视图如图所示，分别
为的中点．
（1）求证：平面；
（2）求多面体的体积；
（3）求证：．
已知函数____________。
下列四种说法：
①命题“x∈R，使得x2＋1＞3x”的否定是“x∈R，都有x2＋1≤3x”；
②“m=－2”是“直线(m＋2)x＋my＋1=0与直线（m－2）x＋(m＋2)y－3=0相互垂直”的必要不充分条件；
③在区间[－2，2]上任意取两个实数a，b，则关系x的二次方程x2＋2ax－b2＋1=0的两根都为实数的概率为；
④过点（，1）且与函数y=图象相切的直线方程是4x＋y－3=0．
其中所有正确说法的序号是____________。
若（为虚数单位），则的值可能是 .
已知等比数列的前项和为
（Ⅰ）求数列的通项公式；
（Ⅱ）设数列满足，为数列 的前项和，试比较 与 的大小，并证明你的结论．
已知是虚数单位，则( )
A． B． C． D．
，在该几何体的正视图中，这条棱的投影是长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为__________
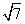，在该几何体的正视图中，这条棱的投影是长为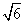的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为__________
的底面
是矩形，
⊥平面
，
为棱
上一点，且
.
的余弦值；
到平面
的距离.
的左右焦点分别为
，线段
被抛物线
的焦点分成
的两段，过点C(-1,0)且以向量
为方向向量的直线
交椭圆于不同两点A,B，满足
的直观图及三视图如图所示，
分别
的中点．
平面
；
的体积；
．
____________。
x∈R，使得x2＋1＞3x”的否定是“
x∈R，都有x2＋1≤3x”；
；
，1）且与函数y=
图象相切的直线方程是4x＋y－3=0． 
（
为虚数单位），则
的
值可能是 .
的前
项和为
满足
，
为数列
与 
的大小，并证明你的结论．
是虚数单位，则
( ) 
B．
C．
D．