题目内容
15.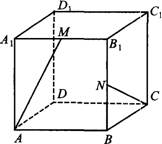 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
分析 如图所示,建立空间直角坐标系.利用向量的夹角公式即可得出.
解答 解:如图所示,建立空间直角坐标系.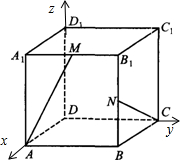
不妨取AB=2,则D(0,0,0),A(2,0,0),M(2,1,2),
C(0,2,0),N(2,2,1),
$\overrightarrow{AM}$=(0,1,2),$\overrightarrow{CN}$=(2,0,1),
∴$cos<\overrightarrow{AM},\overrightarrow{CN}>$=$\frac{\overrightarrow{AM}•\overrightarrow{CN}}{|\overrightarrow{AM}||\overrightarrow{CN}|}$=$\frac{2}{\sqrt{5}×\sqrt{5}}$=$\frac{2}{5}$.
点评 本题考查了空间位置关系、异面直线所成的角、向量的夹角公式、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6.已知复数z满足z(3+4i)=5-5i,则复数z在复平面对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.△ABC中,A=$\frac{π}{6}$,b=2,以下错误的是( )
| A. | 若a=1,则c有一解 | B. | 若a=$\sqrt{3}$,则c有两解 | ||
| C. | 若a=$\frac{11}{6}$,则c有两解 | D. | 若a=3,则c有两解 |
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{f(x-1)+1,x>0}\end{array}\right.$当x∈[0,10]时,关于x的方程f(x)=x的所有解的和为( )
| A. | 50 | B. | 55 | C. | 60 | D. | 65 |
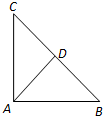 如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )
如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )