题目内容
4.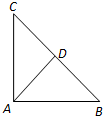 如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )
如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )| A. | (-2,4) | B. | (-2,6) | C. | (0,4) | D. | (0,6) |
分析 在AB上取点P使得AP=$\frac{1}{4}AB$=1,以AP,AC为邻边方向作平行四边形,根据M的位置判断m的取值范围,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{BM}$,代入数量积运算得出$\overrightarrow{AM}•\overrightarrow{BM}$关于m的函数,求出该函数的值域即可.
解答 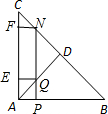 解:在AB上取点P使得AP=$\frac{1}{4}AB$,
解:在AB上取点P使得AP=$\frac{1}{4}AB$,
过P作PN∥AC交AD于Q,交BC于N,分别作AB的平行线NF,EQ.
则M在线段NQ上(不含端点),
∵AB=AC=4,D为BC的中点,
∴AD平分∠BAC.
∴AE=AP=$\frac{1}{4}$AB=1,
$\frac{NP}{AC}=\frac{BP}{AB}=\frac{3}{4}$,∴NP=3,
∴AF=3.
∵$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,
∴$\frac{1}{4}$<m<$\frac{3}{4}$.
∵$\overrightarrow{BM}$=$\overrightarrow{AM}-\overrightarrow{AB}$=-$\frac{3}{4}\overrightarrow{AB}+m\overrightarrow{AC}$,
又$\overrightarrow{AB}•\overrightarrow{AC}$=0,
∴$\overrightarrow{AM}•\overrightarrow{BM}$=($\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$)•(-$\frac{3}{4}\overrightarrow{AB}+m\overrightarrow{AC}$)=-$\frac{3}{16}$${\overrightarrow{AB}}^{2}$+m2${\overrightarrow{AC}}^{2}$=16m2-3,
∵$\frac{1}{4}$<m<$\frac{3}{4}$,∴-2<16m2-3<6.
故选B.
点评 本题考查了平面向量线性运算的几何意义,平面向量的数量积运算,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | y=($\sqrt{x}$)2 | B. | y=a${\;}^{{{log}_a}x}}$ | C. | y=$\left\{\begin{array}{l}x,(x>0)\\-x,(x<0)\end{array}$ | D. | y=$\sqrt{x^2}$ |
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
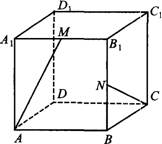 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.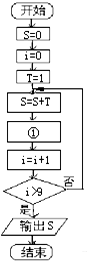 如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.
如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.