题目内容
3.△ABC中,A=$\frac{π}{6}$,b=2,以下错误的是( )| A. | 若a=1,则c有一解 | B. | 若a=$\sqrt{3}$,则c有两解 | ||
| C. | 若a=$\frac{11}{6}$,则c有两解 | D. | 若a=3,则c有两解 |
分析 在△ABC中,已知a,b和角A时,①若A为锐角,有bsin A<a<b,则三角形有两解,②若a=bin A,则有一解,③若a≥b,则有一解,逐一判断各个选项即可得解.
解答 解:∵A=$\frac{π}{6}$,b=2,可得:bsinA=1,
对于A,若a=1,则A为锐角,bsinA=a,可得c有一解,故正确;
对于B,若a=$\sqrt{3}$,则bsinA<a<b,则c有两解,故正确;
对于C,若a=$\frac{11}{6}$,则bsinA<a<b,c有两解,故正确;
对于D,若a=3,则A为锐角,a>b,则c有一解,故不正确;
故选:D.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了三角形解的个数的判断,属于中档题.

练习册系列答案
相关题目
8.已知函数f(x)=4x2-1,若数列{${\frac{1}{f(n)$}前n项和为Sn,则S2018的值为( )
| A. | $\frac{2017}{2018}$ | B. | $\frac{2016}{2018}$ | C. | $\frac{4036}{4037}$ | D. | $\frac{2018}{4037}$ |
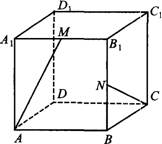 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.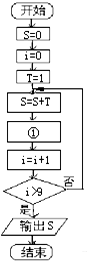 如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.
如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.