题目内容
5.已知,x,y的方程组$\left\{\begin{array}{l}{mx+4y=2}\\{x+y=1}\end{array}\right.$.(1)求D,Dx,Dy;
(2)当实数m为何值时方程组无解;
(3)当实数m为何值时方程组有解,并求出方程组的解.
分析 (1)根据方程组得解法求得D=m-4,Dx=-2,Dy=m-2;
(2)由线性方程组解得存在性,当丨A丨=0时,方程组无解;根据行列式的展开,求得m的值;
(3)由当$|\begin{array}{l}{m}&{4}\\{1}&{1}\end{array}|$≠0,方程组有唯一解,由(1)即可求得方程组的解.
解答 解:(1)$[\begin{array}{l}{m}&{4}\\{1}&{1}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{2}\\{1}\end{array}]$,
D=m-4,Dx=-2,Dy=m-2 (3分)
(2)由A=$[\begin{array}{l}{m}&{4}\\{1}&{1}\end{array}]$,当丨A丨=0,
即$|\begin{array}{l}{m}&{4}\\{1}&{1}\end{array}|$=m-4=0,解得:m=4,
∴当m=4,方程组无解 (5分)
(3)当$|\begin{array}{l}{m}&{4}\\{1}&{1}\end{array}|$≠0,解得:m≠4,方程组有唯一解,
由$\left\{\begin{array}{l}{mx+4y=2}&{①}\\{x+y=1}&{②}\end{array}\right.$,①-4×②解得:y=$\frac{m-2}{m-4}$,代入求得x=$\frac{-2}{m-4}$,
∴方程的解集为:$\left\{\begin{array}{l}{x=\frac{-2}{m-4}}\\{y=\frac{m-2}{m-4}}\end{array}\right.$.
点评 本题考查方程组解得存在性,考查方程组的解与丨A丨的关系,行列式的展开,考查计算能力,属于基础题.

| A. | {1,3} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |
| A. | -2$\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | a=5或a=-$\frac{11}{2}$ | D. | ±2$\sqrt{6}$ |
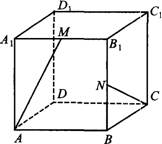 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.