题目内容
6．已知复数z满足z（3+4i）=5-5i，则复数z在复平面对应的点所在的象限为（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 由z（3+4i）=5-5i，得$z=\frac{5-5i}{3+4i}$，然后利用复数代数形式的乘除运算化简复数z，求出复数z在复平面对应的点的坐标，则答案可求．
解答 解：由z（3+4i）=5-5i，
得$z=\frac{5-5i}{3+4i}$=$\frac{（5-5i）（3-4i）}{（3+4i）（3-4i）}=\frac{-5-35i}{25}=-\frac{1}{5}-\frac{7}{5}i$，
则复数z在复平面对应的点的坐标为：（$-\frac{1}{5}$，$-\frac{7}{5}$），位于第三象限．
故选：C．
点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．集合A={-2，-1，0，1，3}，集合B={x|x＞$\frac{1}{2}$ }，则集合A∩（∁RB ） 等于（ ）
| A． | {1，3} | B． | {-2，-1} | C． | {-2，-1，0} | D． | {0，1，3} |
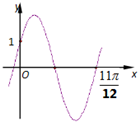已知函数f（x）=2sin（ωx+ϕ）（ω＞0，|ϕ|＜$\frac{π}{2}$）的图象如图所示，则函数f（x）的解析式是f（x）=2sin（2x+$\frac{π}{6}$）．
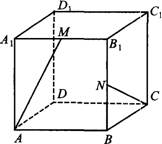在正方体ABCD-A1B1C1D1中，M，N是棱A1B1，B1B的中点，求异面直线AM和CN所成角的余弦值．