题目内容
已知集合A={0,1,2},B={3,4,5},从A中任意取出一个元素a,从B 中任意取出一个元素b,
(1)求点(a,b)落在圆(x-1)2+y2=20内的概率.
(2)求点(a,b)落在平面区域
内的概率.
(1)求点(a,b)落在圆(x-1)2+y2=20内的概率.
(2)求点(a,b)落在平面区域
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)列出事件(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),
其中(0,3),(0,4),(1,3),(1,4),(2,3),(2,4)这6种满足,运用古典概率公式求解即可.
(2)满足
,得出其中(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),(2,4),
这8种情况都满足,运用古典概率公式求解即可.
其中(0,3),(0,4),(1,3),(1,4),(2,3),(2,4)这6种满足,运用古典概率公式求解即可.
(2)满足
|
这8种情况都满足,运用古典概率公式求解即可.
解答:
 解:(1)从A中任意取出一个元素a,从B 中任意取出一个元素b,点(a,b)的所有
解:(1)从A中任意取出一个元素a,从B 中任意取出一个元素b,点(a,b)的所有
可能的取值为:(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),共有9种取值的可能.要使点(a,b)落在圆
(x-1)2+y2=20内(a,b)只需满足(a-1)2+b2<20,
其中(0,3),(0,4),(1,3),(1,4),(2,3),(2,4)这6种满足
(a-1)2+b2<20,∴点(a,b)落在圆(x-1)2+y2=20的概率为
;
(2)要使点(a,b)落在平面区域
内,只需(a,b)满足
,
其中(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),(2,4),
这8种情况都满足
,故所求概率为
.
 解:(1)从A中任意取出一个元素a,从B 中任意取出一个元素b,点(a,b)的所有
解:(1)从A中任意取出一个元素a,从B 中任意取出一个元素b,点(a,b)的所有可能的取值为:(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),共有9种取值的可能.要使点(a,b)落在圆
(x-1)2+y2=20内(a,b)只需满足(a-1)2+b2<20,
其中(0,3),(0,4),(1,3),(1,4),(2,3),(2,4)这6种满足
(a-1)2+b2<20,∴点(a,b)落在圆(x-1)2+y2=20的概率为
| 6 |
| 9 |
(2)要使点(a,b)落在平面区域
|
|
其中(0,3),(0,4),(0,5),(1,3),(1,4),(1,5),(2,3),(2,4),
这8种情况都满足
|
| 8 |
| 9 |
点评:本题考查了基本事件的列取,判断发生事件的个数,结合古典概率公式求解即可,属于中档题.

练习册系列答案
相关题目

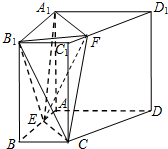 如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.
如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.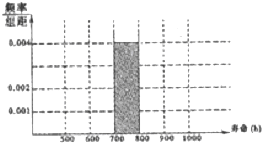 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表:
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表: