题目内容
16.已知i为虚数单位,复数z满足i•z=(1-2i)2,则|z|的值为( )| A. | 2 | B. | 3 | C. | $2\sqrt{3}$ | D. | 5 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简求得z,再由复数模的计算公式求解.
解答 解:由i•z=(1-2i)2,得
$z=\frac{(1-2i)^{2}}{i}=\frac{-3-4i}{i}=\frac{(-3-4i)(-i)}{-{i}^{2}}$=$\frac{-4+3i}{1}=-4+3i$,
∴|z|=$\sqrt{(-4)^{2}+{3}^{2}}=5$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
6.在等差数列{an}中,已知a4=5,a3是a2和a6的等比中项,则数列{an}的前5项的和为( )
| A. | 15 | B. | 20 | C. | 25 | D. | 15或25 |
5.设实数a∈(0,1),则函数f(x)=x2-(2a+1)x+a2+1有零点的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
7.数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),S n为数列{an}前n项和,S100=( )
| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
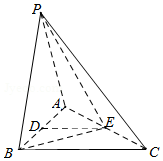 如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$
如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$